今天我们将学习逻辑回归（logistics regression），由于逻辑回归是基于线性回归的特殊变化，故还没有掌握线性回归的小伙伴，可以先点击这里，传送门：《如何用线性回归做数据分析？》

接下来，我将用最简单通俗的语言来为大家介绍逻辑回归模型及其应用。

逻辑回归是解决二分类问题的监督学习算法，用来估计某个类别的概率；其直接预测值是表示0-1区间概率的数据，基于概率再划定阈值进行分类，而求解概率的过程就是回归的过程。

逻辑回归应用于数据分析的场景主要有三种：

• 驱动力分析：某个事件发生与否受多个因素所影响，分析不同因素对事件发生驱动力的强弱（驱动力指相关性，不是因果性）；
• 预测：预测事件发生的概率；
• 分类：适合做多种分类算法、因果分析等的基础组件；

一、逻辑回归的原理

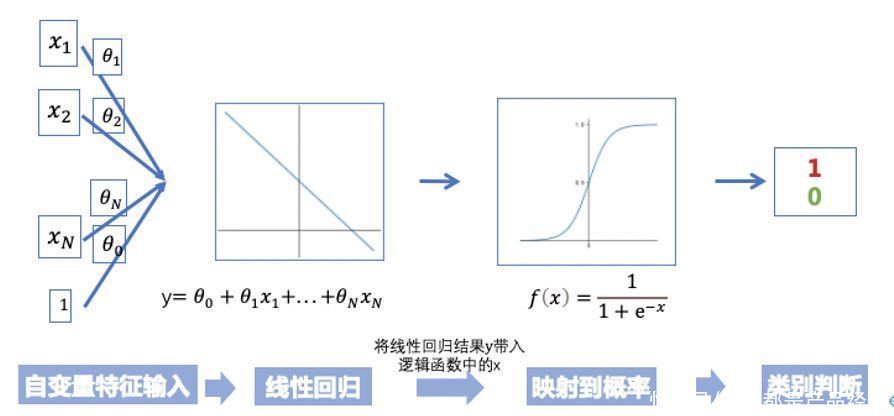
下图是之前讲到的线性回归模型的数据分布，线性回归是用一条线来拟合自变量和因变量之间的关系，我们可以看到其输出结果y是连续的。

例如我们想预测不同用户特征对所使用产品的满意分，可以采用线性回归模型；但是如果我们想根据这些因素去判断用户的性别，或者是否推荐使用等，之前的线性回归就不适用了，这时，我们就要用到逻辑回归进行二分类了。

但是分类模型输出结果却需要是离散的，如何把连续型的y转化为取值范围0-1的数值呢？

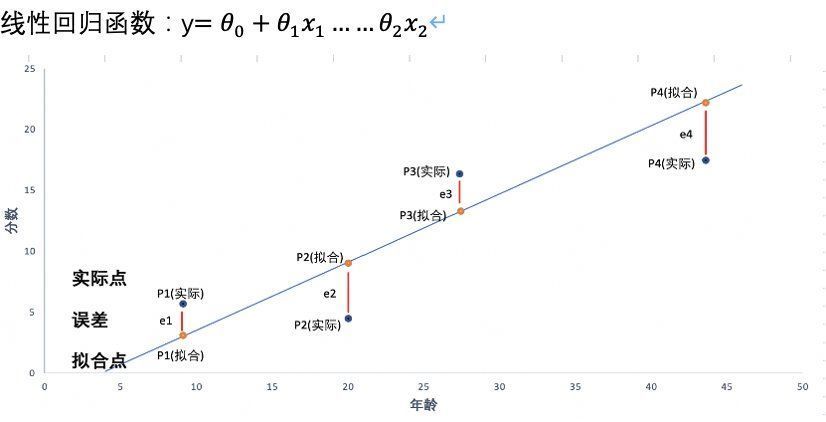
答案是，我们只需要将线性回归模型的结果带入到sigmoid函数（sigmoid函数就是Logistic函数，故本算法名为逻辑回归），即可将线性回归模型转化为二分类问题，这就是逻辑回归。我们可以这样理解：逻辑回归=线性回归+sigmoid函数

那么，什么是sigmoid函数呢？如图，当输入值趋于无穷小时，函数值趋近于0；输入值趋于无穷大时，函数值趋近于1。我们将线性回归结果y带入到sigmoid函数的x，即下图横坐标，就轻而易举的将连续变量y转换为了0-1区间的一个概率值。当这个概率值(函数值)小于0.5时，我们将最终结果预测为0，当概率值大于0.5时，我们将预测结果预测为1。

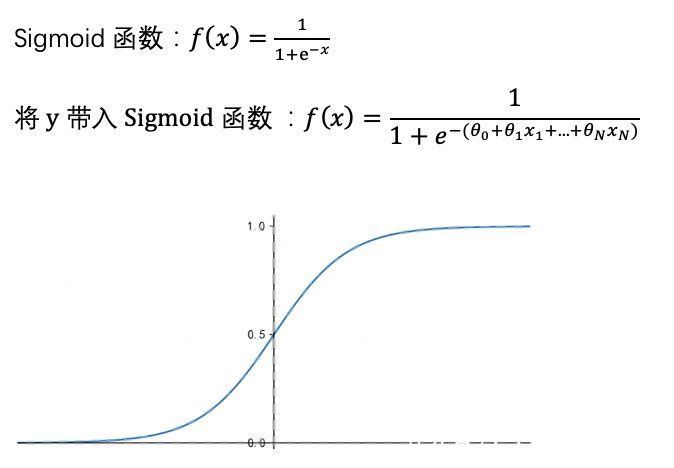
以上就是逻辑回归的基本原理，简述一下逻辑回归的算法步骤，可以概括为四步：

• 将自变量特征输入
• 定义自变量的线性组合y，即针对自变量线性回归
• 将线性回归结果y映射到sigmoid函数，生成一个0-1范围取值的函数概率值
• 根据概率值，定义阈值(通常为0.5)，判定分类结果的正负

二、逻辑回归的目标函数

在明确了逻辑回归的原理后，我们来看它的目标函数可以用什么来表示？在之前的线性回归模型中，我们用误差平方和来做其目标函数，意思就是每个数据点预测值与实际值误差的平方和。在此，我们将单一数据点的误差定义为cost函数，即可获得目标函数的通用形式：

我希望每一个我预测出的数据点结果使得它的误差所带来的代价越小越好，然后求和所得到的目标函数也是越小越好。在具体模型训练的时候，我们在假设可以调整模型的一些参数，通过这些参数我们求得每一点的预测值，最终我们调整模型参数使得目标函数可以取到它能取得的最小值。

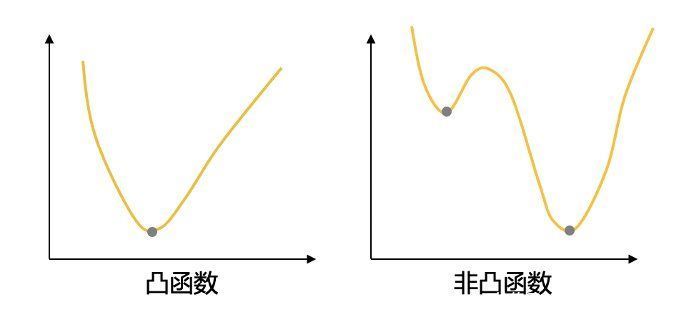
但是逻辑回归不可用最小误差平方和作为其目标函数，原因主要是逻辑回归的优化方法需要使用梯度下降法，而使用误差平方和会导致非凸（non-convex）的目标函数，非凸函数会存在多个局部极小值，而多个局部极小值不利于用梯度下降法找到全局的最小损失值。

那么逻辑回归用什么来表示误差呢？如果y表示样本的真实标签，即0或者1，f(x)表示预测结果是0或者1的概率，f(x)的取值在区间[0,1]。

逻辑回归的cost函数如下，我们如何理解这个公式呢？

当真实标签为正时，即y= 1，Cost函数=-log?(f(x)), 预测值越接近于1，说明预测越准确，则损失函数趋于0。

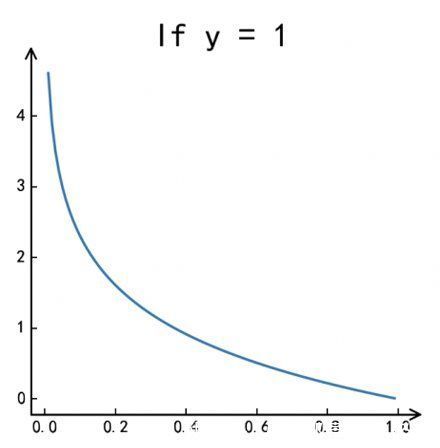
当真实标签为负时，即y= 0，Cost函数=-log?(1-f(x)),预测值越接近于0，说明预测越准确，则损失函数趋于0。